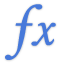
BMR
A BMR függvény a befektetések belső megtérülési rátáját számítja ki, amely a rendszeres időközönként előforduló lehetségesen szabálytalan pénzforgalom sorozatán alapul (olyan fizetések, amelyeknek nem kell állandó összegűeknek lenniük).
BMR(áramlás-tartomány, becslés)
áramlás-tartomány: A pénzforgalom értékeit tartalmazó gyűjtemény. Az áramlás-tartomány csak számértékeket tartalmazhat. A jövedelem (pénzbeáramlás) pozitív számként van megadva, a kiadás (pénzkiáramlás) negatív számként van megadva. A gyűjteményben legalább egy pozitív és egy negatív értéknek szerepelnie kell. A pénzforgalomnak időrendi sorrendben és rendszeres időközönként kell szerepelnie (például havonta). Ha egy időszakban nincs pénzforgalom, használjon az időszakhoz 0 értéket.
becslés: A megtérülési ráta kezdeti becslését megadó opcionális számérték. A becslés tizedesjeggyel (például 0,08) vagy százalékos formában (például 8%) van megadva. Ha a becslés nincs megadva, a függvény 10% értéket feltételez. Ha az alapértelmezett érték nem hoz eredményt, kezdetben próbáljon ki nagyobb pozitív értéket. Ha ez sem hoz eredményt, próbálkozzon kis negatív értékkel. A minimális engedélyezett érték a –1.
Megjegyzések
Ha az összes periodikus pénzforgalom mindig azonos, fontolja meg az NMÉ függvény használatát.
A függvény eredményeként megjelenő pénznem a Nyelv és régió beállításaitól (macOS-ben a Rendszerbeállítások, iOS-ben és iPadOS-ben a Beállítások alatt), vagy az iCloud Időzóna / Régió beállításaitól függ.
1. példa |
|---|
Tegyük fel, hogy a lánya egyetemi képzését tervezgeti. Most lett 13 éves, és várhatóan 5 év múlva fogja elkezdeni az egyetemet. Ma 75 000 dollárnyi megtakarított pénze van egy takarékbetét-számlán, és a munkaadójától kapott bónuszt is hozzáadja minden év végén. Mivel úgy gondolja, hogy a bónusz minden évben növekedni fog, várakozásai szerint év végén rendben 5000, 7000, 8000, 9000 és 10 000 dollárt tud majd félretenni a következő 5 évben. Számításai szerint 150 000 dollárt kell félretennie az oktatásra, mire a lánya eléri az egyetemi életkort. Tegyük fel, hogy a B2–G2 cellák tartalmazzák a befizetendő összegeket az első befizetéssel kezdve, negatív összegként, mivel ezek pénzkiáramlások (-75 000, -5000, -7000, -8000, -9000, -10 000). A H2 cella azt az összeget tartalmazza, amelyre a becslése szerint szüksége lesz a lánya egyetemi oktatásának finanszírozásához. Az összeg pozitív számként van kifejezve, mert pénzbeáramlásnak számít (150 000). Az áramlás-tartomány értéke B2:H2. A =BMR(B2:H2) eredménye 5,69965598016224%, az ahhoz szükséges tőkésített kamatláb, hogy a befizetett összegek az éves kamattal együtt 5 év alatt 150 000 dollárra nőjenek. |
2. példa |
|---|
Tegyük fel, hogy lehetősége van egy társulásba pénzt befektetni. A szükséges kezdeti befektetés összege 50 000 dollár. Mivel a társulás még fejleszti a termékét, további 25 000 dollárt, illetve 10 000 dollárt kell befektetni az első és a második év végén. Tegyük fel, hogy ezeket a pénzkiáramlásokat negatív számokként a B3–D3 cellákba helyezi. A harmadik évben a társulás várhatóan önfinanszírozó lesz, de a befektetőknek nem térít vissza pénzt (0 az E3 cellában). A negyedik és ötödik években a befektetők előreláthatóan 10 000 és 30 000 dollárt fognak kapni (az F3 és a G3 cellákban pozitív számként). A hatodik év végére a vállalatot várhatóan eladják, és a befektetők 100 000 dollárt fognak kapni (a H3 cellában pozitív számként). A =BMR(B3:H3) eredménye 10,2411564203%, az elért tőkésített évi kamatláb (a belső megtérülési ráta), feltételezve, hogy az összes pénzforgalom az ütemezésnek megfelelően történik. |