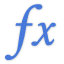
FV
הפונקציה FV מחשבת את הערך העתידי של השקעה בהתאם לסדרה של תזרימי מזומנים תקופתיים קבועים (תשלומים של סכום קבוע, וכן כל תזרימי המזומנים שמתבצעים במרווחי זמן קבועים) ושיעור ריבית קבוע.
FV(שיעור-תקופתי, מספר-תקופות, תשלום, ערך-נוכחי, תאריך-היעד)
שיעור-תקופתי: ערך מספרי המייצג את שיעור הריבית לכל התקופה. שיעור-תקופתי מוזן כמספר עשרוני (לדוגמה, 0.08) או עם סימן אחוז (לדוגמה, 8%). שיעור-תקופתי מוגדר באמצעות אותה מסגרת זמן (לדוגמה, מדי חודש, מדי רבעון או מדי שנה) כמספר-תקופות. לדוגמא, אם מספר-תקופות מייצג חודשים ושיעור הריבית השנתית עומד על 8%, יש לציין את שיעור-תקופתי כ-0.00667 או 0.667% (0.08 לחלק ל-12). שיעור-תקופתי יכול להיות שלילי, אך התוצאה המוחזרת על-ידי הפונקציה עלולה להיות קשה לפירוש.
מספר-תקופות: ערך מספרי המייצג את מספר התקופות. מספר-תקופות מוגדר באמצעות אותה מסגרת זמן (לדוגמא, חודשי, רבעוני או שנתי) כשיעור-תקופתי. על מספר-תקופות להיות גדול מ-0 או שווה לו.
תשלום: ערך מספרי המייצג את התשלום שבוצע או הסכום שהתקבל בכל תקופה. תשלום מעוצב בדרך כלל כמטבע. בכל תקופה, סכום שמתקבל הוא סכום חיובי וסכום שמושקע הוא סכום שלילי. למשל, יתכן שמדובר בהחזר חודשי של הלוואה (שלילי) או בתשלום תקופתי שהתקבל בגין קצבה (חיובי).
ערך-נוכחי: ערך מספרי המייצג את ההשקעה ההתחלתית, או את הסכום של ההלוואה או הקצבה. ערך-נוכחי מעוצב בדרך כלל כמטבע. בזמן 0, סכום שמתקבל הוא סכום חיובי וסכום שמושקע הוא סכום שלילי. למשל, יתכן שמדובר בסכום שנלקח כהלוואה (חיובי) או בתשלום הראשון של חוזה של קצבה (שלילי). אם הערך תשלום מוגדר ואין השקעה התחלתית, ניתן להשמיט את הערך ערך-נוכחי.
תאריך-היעד: ערך מודאלי אופציונלי המגדיר אם התשלומים יבוצעו בהתחלה או בסוף של כל תקופה. במקרה של רוב המשכנתאות והלוואות אחרות, יש לבצע את התשלום הראשון בסוף התקופה הראשונה (0), ואפשרות זו מוגדרת כברירת-המחדל. מרבית תשלומי החכירה וההשכרה, וכמה סוגים אחרים של תשלומים, מתבצעים בתחילת כל תקופה (1).
סיום(0 או מושמט): התשלום ייחשב לתשלום שהתקבל או התבצע בסוף כל תקופה.
התחלה (1): התשלום ייחשב לתשלום שהתקבל או התבצע בהתחלה של כל תקופה.
הערות
סוג המטבע המוצג בתוצאת פונקציה זו נקבע לפי הגדרות ״שפה ואזור״ (ב״העדפות המערכת״ ב-macOS וב״הגדרות״ ב-iOS וב-iPadOS) או בהגדרות ״שעון מקומי ואזור״ בהגדרות iCloud.
דוגמא 1 |
|---|
נניח שהינך מתכנן/ת לחסוך ללימודים של בתך באוניברסיטה. בדיוק מלאו לה 3 שנים, והיא צפויה להתחיל את לימודיה בעוד 15 שנים. יש לך $50,000 (ערך-נוכחי עומד על -50000) שבאפשרותך לשים בצד בחשבון חיסכון היום, ותוכל/י להוסיף $200 (תשלום הוא -200) לחשבון בתחילת כל חודש (תאריך היעד הוא 1). במהלך 15 השנים הבאות (מספר תקופות הוא 15*12), חשבון החיסכון צפוי לצבור ריבית שנתית של 4.5% (שיעור-תקופתי הוא 0.045/12), והריבית תשולם מדי חודש. =FV(0.045/12, 15*12, -200, -50000, 1) תחזיר את התוצאה $149,553.00, הערך הצפוי של חשבון החיסכון כאשר בתך תתחיל את לימודיה באוניברסיטה. |
דוגמא 2 |
|---|
נניח שהוצגה בפניך הזדמנות להשקעה. ההזדמנות דורשת שתשקיע/י היום $50,000 בנייר ערך בניכיון (ערך-נוכחי הוא -50000) ולא תידרש/י להשקיע שום דבר בהמשך (תשלום הוא 0). הפרעון של נייר הערך בניכיון יחול בעוד 14 שנה (מספר-תקופות) והתשלום שיתקבל במועד הפרעון יעמוד על $100,000. לחלופין, תוכל/י להשאיר את הכסף בחשבון החיסכון שלך בשוק הכסף, שם התשואה השנתית שלו צפויה לעמוד על 5.25% (שיעור-תקופתי). דרך אחת להעריך הזדמנות זו היא לחשב כמה $50,000 יהיו שווים בסוף תקופת ההשקעה ולהשוות סכום זה לערך הפדיון של נייר הערך. =FV(0.0525, 14, 0, -50000, 0) תחזיר את התוצאה $102,348.03, הערך העתידי של החשבון בשוק הכסף בתום 14 שנים, בהנחה ששיעור הריבית השנתית יעמוד על 5.25%. לפיכך, בהנחה שכל שאר הגורמים שווים, ושכל ההנחות יתממשו כמצופה, האפשרות העדיפה היא להשאיר את הכסף בחשבון בשוק הכסף מכיוון שהערך שלו בתום 14 שנים ($102,348.03) גבוה מערך הפדיון של נייר הערך ($100,000). |