Hjælp til formler og funktioner
- Velkommen
- Introduktion til formler og funktioner
-
- PÅLØBRENTE
- PÅLØBRENTE.UDLØB
- VARIGHED
- MVARIGHED
- KUPONDAGE.SA
- KUPONDAGE.A
- KUPONDAGE.ANK
- KUPONBETALINGER
- AKKUM.RENTE
- AKKUM.HOVEDSTOL
- VALUTA
- VALUTAKODE
- VALUTAKONVERTERING
- VALUTAH
- DB
- DSA
- DISKONTO
- EFFEKTIV.RENTE
- FV
- RENTEFOD
- R.YDELSE
- IA
- ISPMT
- MIA
- NOMINEL
- NPER
- NUTIDSVÆRDI
- YDELSE
- H.YDELSE
- KURS
- KURS.DISKONTO
- KURS.UDLØB
- NV
- RENTE
- MODTAGET.VED.UDLØB
- LA
- VÆRDIPAPIR
- VÆRDIPAPIRH
- ÅRSAFSKRIVNING
- VSA
- XIRR
- XNPV
- AFKAST
- AFKAST.DISKONTO
- AFKAST.UDLØBSDATO
-
- ABS
- AFRUND.LOFT
- KOMBIN
- LIGE
- EKSP
- FAKULTET
- DOBBELT.FAKULTET
- AFRUND.GULV
- STØRSTE.FÆLLES.DIVISOR
- HELTAL
- MINDSTE.FÆLLES.MULTIPLUM
- LN
- LOG
- LOG10
- REST
- MAFRUND
- MULTINOMIAL
- ULIGE
- PI
- POLYNOMIUM
- POTENS
- PRODUKT
- KVOTIENT
- SLUMP
- SLUMPMELLEM
- ROMERTAL
- AFRUND
- RUND.NED
- RUND.OP
- SERIESUM
- FORTEGN
- KVROD
- KVRODPI
- SUBTOTAL
- SUM
- SUM.HVIS
- SUM.HVISER
- SUMPRODUKT
- SUMKV
- SUMX2MY2
- SUMX2PY2
- SUMXMY2
- AFKORT
-
- MAD
- MIDDEL
- MIDDELV
- MIDDEL.HVIS
- MIDDEL.HVISER
- BETAFORDELING
- BETAINV
- BINOMIALFORDELING
- CHIFORDELING
- CHIINV
- CHITEST
- KONFIDENSINTERVAL
- KORRELATION
- TÆL
- TÆLV
- ANTAL.BLANKE
- TÆL.HVIS
- TÆL.HVISER
- KOVARIANS
- KRITBINOM
- SAK
- EKSPFORDELING
- FFORDELING
- FINV
- PROGNOSE
- FREKVENS
- GAMMAFORDELING
- GAMMAINV
- GAMMALN
- GEOMIDDELVÆRDI
- HARMIDDELVÆRDI
- SKÆRING
- STØRSTE
- LINREGR
- LOGINV
- LOGNORMFORDELING
- MAKS
- MAKSV
- MAKSHVISER
- MEDIAN
- MIN
- MINV
- MINHVISER
- HYPPIGST
- NEGBINOMFORDELING
- NORMFORDELING
- NORMINV
- STANDARDNORMFORDELING
- STANDARDNORMINV
- FRAKTIL
- PROCENTPLADS
- PERMUT
- POISSON
- SANDSYNLIGHED
- KVARTIL
- PLADS
- STIGNING
- MINDSTE
- STANDARDISER
- STDAFV
- STDAFVV
- STDAFVP
- STDAFVPV
- TFORDELING
- TINV
- TTEST
- VARIANS
- VARIANSV
- VARIANSP
- VARIANSPV
- WEIBULL
- ZTEST
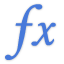
CHITEST
Funktionen CHITEST returnerer værdien fra chi2-fordelingen af de givne data. Alle værdier er talværdier.
CHITEST(faktiske-værdier; forventede-værdier)
faktiske-værdier: Den samling, som indeholder de faktiske værdier.
forventede-værdier: Den samling, som indeholder de forventede værdier.
Noter
De frihedsgrader, der hører til den returnerede værdi, er antallet af rækker i faktiske-værdier minus 1.
Hver forventet værdi beregnes ved at gange summen af rækken med summen af kolonnen og dividere med den samlede total.
Eksempel |
|---|
Antag, at det mulige svarudsnit til et bestemt spørgsmål i en undersøgelse var 1 til 5. Undersøgelsens resultater blev akkumuleret separat for mænd og kvinder. I den følgende tabel indeholder cellerne B3:C7 det faktiske antal, der har valgt hvert svar, fordelt på mænd og kvinder. Cellerne B9:C13 indeholder den beregnede populations forventede værdier for en normal population, baseret på eksemplet. Hver populations forventede værdi beregnes ved at gange summen af rækken med summen af kolonnen og dividere med den samlede total. |
A | B | C | |
|---|---|---|---|
1 | Svar | Mænd | Kvinder |
2 | Faktisk | Valgt | Valgt |
3 | 5 | 15 | 9 |
4 | 4 | 56 | 35 |
5 | 3 | 11 | 23 |
6 | 2 | 10 | 23 |
7 | 1 | 8 | 10 |
8 | Forventet | Valgt | Valgt |
9 | 5 | 12,00 | 4,50 |
10 | 4 | 10,20 | 3,83 |
11 | 3 | 4,92 | 1,85 |
12 | 2 | 4,82 | 1,81 |
13 | 1 | 4,21 | 1,58 |
=CHITEST(B3:C7; B9:C13) returnerer ca. 1,3382569E-218. Med denne værdi og frihedsgraderne (4 i dette eksempel, fordi der er 5 rækker med faktiske værdier) kan du bruge en chi-kvadrattabel til at bestemme, om der er en statistisk signifikant forskel mellem eksempelresultatet og det forventede populationsresultat. |