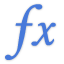
FV
Funkcija FV vraća buduću vrijednost ulaganja na temelju niza pravilnih periodičnih novčanih tijekova (isplate konstantnog iznosa i svih novčanih tijekova u konstantnim intervalima) te fiksne kamatne stope.
FV(periodična-kamata, br-periodi, plaćanje, sadašnja-vrijednost, kada-izvršenje)
periodična-kamata: Brojčana vrijednost koja predstavlja kamatnu stopu po razdoblju. periodična-kamata može se unijeti kao decimalni broj (na primjer, 0,08) ili sa znakom postotka (na primjer, 8%). periodična-kamata određuje se s pomoću istog vremenskog okvira (primjerice, mjesečno, kvartalno ili godišnje) kao br-periodi. Na primjer, ako br-periodi predstavlja mjesece, a godišnja kamatna stopa iznosi 8%, periodična-kamata navodi se kao 0,00667 ili 0,667% (0,08 podijeljeno s 12). periodična-kamata može biti negativna, ali rezultat koji vraća funkcija možda će se teško interpretirati.
br-periodi: Brojčana vrijednost koja predstavlja broj perioda. br-periodi određuje se s pomoću istog vremenskog okvira (primjerice, mjesečno, kvartalno ili godišnje) kao periodična-kamata. br-periodi mora biti veća ili jednaka nuli.
plaćanje: Brojčana vrijednost koja predstavlja plaćanje koje je izvršeno ili iznos koji se prima u svakom razdoblju. plaćanje obično se formatira kao valuta. U svakom razdoblju, primljeni je iznos pozitivan iznos, a uloženi je iznos negativan iznos. Na primjer, to bi moglo biti mjesečno plaćanje kredita (negativno) ili periodični iznos primljen na temelju anuiteta (pozitivno).
sadašnja-vrijednost: Brojčana vrijednost koja predstavlja inicijalne investicije ili iznos kredita ili rate. sadašnja-vrijednost obično se formatira kao valuta. Kada je vrijeme 0, primljeni je iznos pozitivan iznos, a uloženi je iznos negativan iznos. Na primjer, to bi mogao biti posuđeni iznos (pozitivan) ili početna isplata na temelju ugovora o anuitetu (negativna). Ako je plaćanje određeno i nema početnog ulaganja, sadašnja-vrijednost može se izostaviti.
kada-izvršenje: Opcionalna modalna vrijednost koja određuje hoće li se plaćanje vršiti na početku ili na kraju svakog razdoblja. Većina hipoteka i ostalih kredita zahtijevaju prvu uplatu na kraju prvog razdoblja (0), koje je standardno. Većina plaćanja zakupa i najmova te neki ostali tipovi plaćanja dospijevaju na početku svakog razdoblja (1).
kraj(0 ili izostavljeno): Plaćanje se smatra primljenim ili izvršenim na kraju svakog razdoblja.
početak (1): Plaćanje se smatra primljenim ili izvršenim na početku svakog razdoblja.
Napomene
Valuta prikazana u ovom rezultatu funkcije ovisi o postavkama Jezik i Regija (u Postavkama sustava u sustavu macOS i u Postavkama u sustavu iOS i iPadOS) ili o postavkama Vremenska zona i Regija u Postavkama iClouda).
1. primjer |
|---|
Zamislite da planirate fakultetsko obrazovanje za svoju kćer. Tek je napunila 3 godine i očekujete da će upisati fakultet za 15 godina. Imate 50.000 $ (sadašnja-vrijednost je -50000) koje danas možete uplatiti na štedni račun te možete dodavati 200 $ (plaćanje je -200) na račun na početku svakog mjeseca (kada-izvršenje je 1). Tijekom sljedećih 15 godina (br-periodi iznosi 15*12), očekuje se da će na račun sjesti godišnja kamatna stopa od 4,5% (periodična-kamata iznosi 0,045/12), te svaki mjesec donosi kamate. =FV(0,045/12; 15*12; -200; -50000; 1) vraća 149.553,00 $, očekivanu vrijednost štednog računa kada vaša kći upiše fakultet. |
2. primjer |
|---|
Zamislite da vam se pruži prilika za ulaganje. Ta prilika zahtijeva da danas uložite 50.000 $ u diskontnu vrijednosnicu (sadašnja-vrijednost je -50000), a zatim više ništa (plaćanje je 0). Diskontna vrijednosnica dospijeva za 14 godina (br-periodi) i vratit će 100.000 $ po dospijeću. Druga vam je mogućnost ostaviti novac na vašem štednom računu na tržištu novca gdje se očekuje da će zaraditi godišnji prinos od 5,25% (periodična-kamata). Jedan od načina vrednovanja ove prilike bio bi uzeti u obzir koliko bi 50.000 $ vrijedilo na kraju investicijskog razdoblja i usporediti to s otkupnom vrijednošću vrijednosnice. =FV(0,0525; 14; 0; -50000; 0) vraća 102.348,03 $, buduću vrijednost računa na tržištu novca na kraju razdoblja od 14 godina, pod pretpostavkom da godišnja kamatna stopa iznosi 5,25%. Dakle, s obzirom da je sve ostalo jednako, te ako se sve pretpostavke ostvare prema očekivanjima, bilo bi bolje zadržati novac na računu na tržištu novca jer njegova vrijednost nakon 14 godina (102.348,03 $) premašuje otkupnu vrijednost vrijednosnice (100.000 $). |