
Link text boxes in Pages on iPad
You can link two or more text boxes so that text can flow from one text box to the next. For example, if you’re creating a newsletter you could link text boxes and use them to create irregular columns of text, or continue a sidebar onto another page.
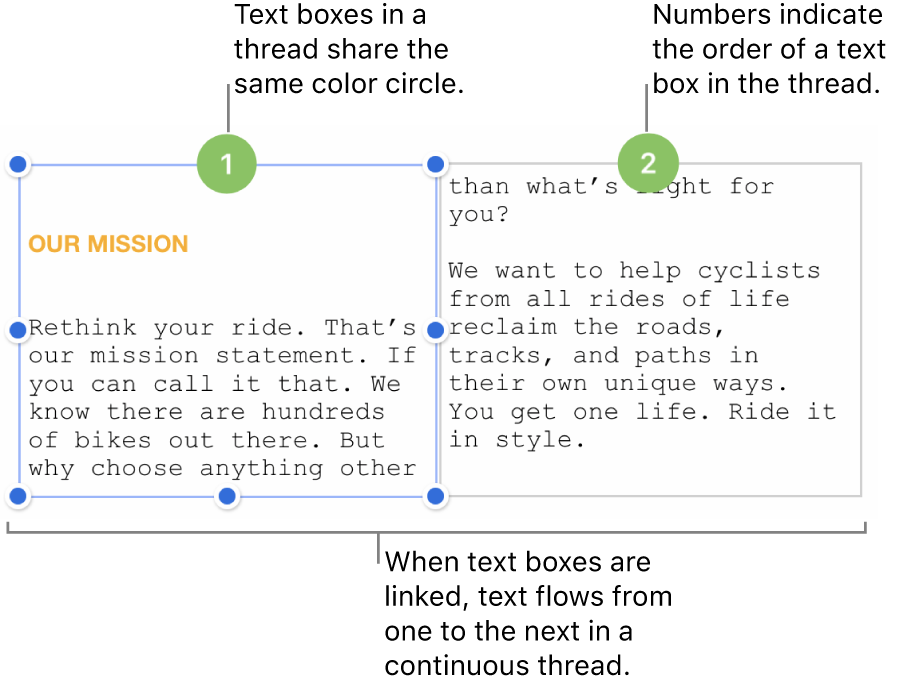
Each series of linked text boxes is called a thread and is identified by the shared color of the circle at the top of each text box. Numbers in the circles indicate the order of the text boxes in the thread. You can add and remove text boxes from a thread, change their order in the thread, move them to a different thread, and more.
Note: Text boxes that are locked or grouped with other objects can’t be linked.
Create a new thread
You can start a thread with an empty text box or one that already has content. For example, if you want to set the documentʼs layout before you add content, you can add several text boxes, place them where you want, then link them. Or, you can start with a text box that already has content, then link more text boxes to accommodate your text.
Tap the text box that you want to be first in the thread, then tap the white circle at the top.

The circle fills with color and the number 1 to indicate it’s the start of a thread. If you see a different number or if the color matches an existing thread, the text box was linked to an existing thread instead. To make it the start of a new thread, tap its circle and choose Create New Thread.
For each additional text box you add to the thread, do one of the following:
Link to an empty text box: Tap the text box, then tap the white circle at the top.
Link to a text box that contains text (and merge the text): Tap the text box containing the text, then tap the circle at the top—this starts a new thread. Tap the circle again, choose the thread you want the text box to belong to, then tap Merge (which adds the content to the end of the thread). You see the Merge dialog only the first time you merge text boxes—after that, content is automatically merged.
The circle of each text box you add fills with the same color shown in the first box, and a number indicates its order in the thread (you can reorder text boxes at any time).
To add content to the thread, type in the first text box of an empty thread, or add to existing text in the thread.
If the last text box in the thread has a clipping indicator
 at the bottom, which indicates that there is more text than can fit in the text box, do one of the following:
at the bottom, which indicates that there is more text than can fit in the text box, do one of the following:Drag the clipping indicator or any resize handle until all the text is visible.
Drag the resize handles of other text boxes in the thread until your text fits into the existing text boxes.
Add another text box to the thread.
Reorder linked text boxes
If a thread has more than one linked text box on a page and you drag one of the text boxes to a new location on the same page, the text box’s content doesn’t automatically reflow to reflect the new location. If you assign a new order to the text box instead, its content reflows naturally.
Tap the text box whose order you want to change, then tap the circle at the top.
Tap Layout Order, then choose a new order number for the text box.
The text in the thread updates to reflect the new order.
When a thread spans more than one page and you move a text box to a different page, the numbering of all of the text boxes in the thread automatically adjusts so the text flows naturally.
Assign a text box to a different thread
You might want to reassign a text box if its placement on the page makes it ideal for another thread and you donʼt want to rearrange the items on your page, or if you simply linked to the wrong thread.
If the text box is the only one in the thread, it and its content are added to the new thread. If the text box is one of several in a thread, only the text box is reassigned to the new thread—its content is reflowed in the remaining text boxes of its original thread.
Tap the text box that you want to reassign, then tap the circle at the top.
Tap the thread you want the text box to belong to.
If you see a dialog asking if you want to merge the content, tap Merge. You see the Merge dialog only the first time you merge text boxes—after that, content is merged automatically.
The text box is added to the thread based on its position on the page. You may need to move or reorder text boxes so the text flows naturally.
Start a new thread from a linked text box
You can start a new thread with a text box that’s already linked to a thread. The text box is unlinked from its original thread and emptied; any text it contained is merged into the remaining text boxes in the original thread.
You might want to do this, for example, if the placement of a linked text box is where you want to start a new thread and you don’t want to change the page layout.
Tap the text box, then tap the circle at the top.
Tap Create New Thread.
Change the style of all text in a thread
You can make style changes to all of the text in a thread at one time.
Place the insertion point in the text of one of the text boxes in the thread.
If any text is selected, formatting changes will apply only to that text.
Tap the insertion point, then tap Select All.
Tap
 in the toolbar, then tap Text to use controls for changing the font, font size, text color, and more.
in the toolbar, then tap Text to use controls for changing the font, font size, text color, and more.
Unlink a text box
When you unlink a text box, if there are other text boxes in the thread, its text is merged into them. If it’s the only text box in the thread, it becomes a standard text box with content.
Tap the text box, tap the circle at the top, then tap Remove from Thread.
Delete a linked text box
When you delete a linked text box, its text is merged into any remaining text boxes in the thread. If it’s the only text box in the thread, the text box and its contents are deleted.
Tap the text box, then tap Delete.
Lock or unlock a text box
To prevent a text box from being moved accidentally, you can lock it. Locking one text box locks all text boxes in that thread. Similarly, if you unlock one text box, they’re all unlocked. While the thread is locked, you can’t make any changes to its formatting or contents.
Lock: Tap
 in the toolbar, tap Arrange, then tap Lock.
in the toolbar, tap Arrange, then tap Lock.Unlock: Tap one of the locked text boxes, then tap Unlock.
Note: Linked text boxes are always set to Stay on Page to help you control where your threads are positioned. See Place objects with text.