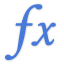
CHITEST

Die Funktion CHITEST berechnet die Wahrscheinlichkeit bei der Chi-Quadrat-Verteilung beim Vergleich zwischen beobachteten und erwarteten Werten. Alle Werte sind numerische Werte.

CHITEST(Istwerte; erwartete Werte)

Istwerte: Die Sammlung, die die Istwerte enthält.

Erwartete Werte: Dies ist die Sammlung der erwarteten Werte.

Hinweise

Der Freiheitsgrad für den Ergebniswert entspricht der Anzahl der Zeilen des Arguments Istwerte abzüglich 1.
Jeder erwartete Wert wird berechnet, indem die Summe der entsprechenden Zeile mit der Summe der zugehörigen Spalte multipliziert und das Produkt durch die Gesamtsumme dividiert wird.

Beispiel
Angenommen, bei einer Umfrage können für eine bestimmte Frage die Werte 1 bis 5 als Antwort angegeben werden. Die Umfrageergebnisse werden für Männer und Frauen getrennt summiert. In der folgenden Tabelle enthalten die Zellen B3:C7 die tatsächliche Zahl der Antworten auf jede Frage getrennt nach Männern und Frauen. Die Zellen B9:C13 enthalten die erwarteten Werte für eine normale Population (Grundgesamtheit) basierend auf der Stichprobe. Jeder für die Population erwartete Wert wird berechnet, indem die Summe der entsprechenden Zeile mit der Summe der zugehörigen Spalte multipliziert und das Produkt durch die Gesamtsumme dividiert wird.

Beispiel

Angenommen, bei einer Umfrage können für eine bestimmte Frage die Werte 1 bis 5 als Antwort angegeben werden. Die Umfrageergebnisse werden für Männer und Frauen getrennt summiert. In der folgenden Tabelle enthalten die Zellen B3:C7 die tatsächliche Zahl der Antworten auf jede Frage getrennt nach Männern und Frauen.

Die Zellen B9:C13 enthalten die erwarteten Werte für eine normale Population (Grundgesamtheit) basierend auf der Stichprobe. Jeder für die Population erwartete Wert wird berechnet, indem die Summe der entsprechenden Zeile mit der Summe der zugehörigen Spalte multipliziert und das Produkt durch die Gesamtsumme dividiert wird.

	A	B	C
1	Antwort	Männer	Frauen
2	Istwerte	Antworten	Antworten
3	5	15	9
4	4	56	35
5	3	11	23
6	2	10	23
7	1	8	10
8	Erwartete Werte	Antworten	Antworten
9	5	12,00	4,50
10	4	10,20	3,83
11	3	4,92	1,85
12	2	4,82	1,81
13	1	4,21	1,58

=CHITEST(B3:C7; B9:C13) liefert den Näherungswert 1,3382569E-218. Mit diesem Wert und den Freiheitsgraden (in diesem Beispiel 4, da es 5 Zeilen mit Istwerten gibt) könntest du anhand einer Tabelle der Chi-Quadrat-Verteilung feststellen, ob es eine statistisch signifikante Differenz zwischen dem Ergebnis der Stichprobe und dem erwarteten Ergebnisse für die Grundgesamtheit gibt.

Vgl. auchCHIVERT CHIINV

Hilfreich?

Formeln und Funktionen-Hilfe

CHITEST

Hinweise