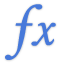
TIR
A função TIR tem como resultado a taxa interna de rentabilidade de um investimento que se baseia numa série de cash-flows potencialmente irregulares (pagamentos que não precisam de ser um montante constante) que ocorrem em intervalos de tempo regulares.
TIR(intervalo-flows; estimativa)
intervalo-flows: Uma coleção que contém os valores de cash-flow. intervalo-flows deve conter valores numéricos. A receita (cash inflow) é especificada como um número positivo e uma despesa (um cash outflow) é especificada como um número negativo. A coleção tem de incluir, pelo menos, um valor positivo e um negativo. Os cash-flows têm de ser especificados por ordem cronológica e em intervalos regulares (por exemplo, todos os meses). Se um período não tiver um cash-flow, use 0 para esse período.
estimativa: Um valor numérico opcional que especifica a estimativa inicial da taxa de rentabilidade. estimativa é introduzida como um valor decimal (por exemplo, 0,08) ou com um sinal de percentagem (por exemplo, 8%). Se estimativa for omitida, é considerada 10%. Se o valor predefinido não resultar numa solução, experimente inicialmente um valor positivo maior. Se isto não der um resultado, experimente um valor negativo pequeno. O valor mínimo permitido é -1.
Notas
Se todos os cash-flows (fluxos monetários) periódicos forem iguais, considere utilizar a função VAL.
A moeda apresentada no resultado desta função depende das definições de Idioma e Região (em Preferências do Sistema no macOS e em Definições no iOS e iPadOS) ou das definições de “Fuso horário e Região” em Definições de iCloud.
Exemplo 1 |
|---|
Imagine que está a planear a educação universitária da sua filha. Ela acabou de fazer 13 anos e espera que ela entre na universidade dentro de 5 anos. Tem 75 000 euros para colocar numa conta poupança hoje e fará um reforço da conta com o bónus que receberá da entidade patronal no final de cada ano. Uma vez que acredita num aumento do bónus todos os anos, prevê que seja possível colocar de parte 5000, 7000, 8000, 9000 e 10 000 euros, respetivamente, no final de cada um dos próximos 5 anos. Pensa que será necessário ter 150 000 euros de parte para a educação da sua filha na altura em que ela entrar na universidade. Assuma que as células B2 a G2 contêm os montantes que irá depositar, como quantias negativas por serem saídas de cash-flow, com início no depósito inicial (-75 000, -5000, -7000, -8000, -9000, -10 000). A célula H2 contém o montante que calculou como necessário para financiar os estudos superiores da sua filha, como número positivo por se tratar de uma entrada de cash-flow (150 000). intervalo-flows é B2:H2. =TIR(B2:H2) tem como resultado 5,69965598016224%, a taxa de juro composta para as quantias depositadas, em conjunto com os juros anuais, atingirem 150 000 euros em cinco anos 5. |
Exemplo 2 |
|---|
Imagine que lhe surge uma oportunidade de investimento numa parceria. O investimento inicial necessário é 50 000 euros. Dado que a parceria está ainda a desenvolver o produto, é necessário investir adicionalmente 25 000 e 10 000 euros no final do primeiro e do segundo ano respetivamente. Assuma que coloca estas saídas de cash-flow, como números negativos, nas células B3 a D3. No terceiro ano, a parceria prevê atingir autonomia financeira, mas sem qualquer reembolso aos investidores (0 em E3). No quarto e quinto ano, está previsto os investidores receberem 10.000 e 30.000 euros respetivamente (como números positivos em F3 e G3). No final do sexto ano, a empresa espera vender e está previsto os investidores receberem 100.000 euros (como número positivo em H3). =TIR(B3:H3) tem como resultado 10,2411564203%, a taxa de juro anual composta obtida (taxa de rendimento interna) assumindo que todos os cash-flows ocorrem conforme está previsto. |