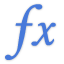
PV
The PV function returns the present value of an investment or annuity based on a series of regular periodic cash flows (payments of a constant amount and all cash flows at constant intervals) and at a fixed interest rate.
PV(periodic-rate, num-periods, payment, future-value, when-due)
periodic-rate: A number value representing the interest rate per period. periodic-rate is entered as a decimal (for example, 0.08) or with a per cent sign (for example, 8%). periodic-rate is specified using the same time frame (for example, monthly, quarterly or annually) as num-periods. For example, if num-periods represents months and the annual interest rate is 8%, periodic-rate is specified as 0.00667 or 0.667% (0.08 divided by 12). periodic-rate can be a negative value, but the result returned by the function may be difficult to interpret.
num-periods: A number value representing the number of periods. num-periods is specified using the same time frame (for example, monthly, quarterly or annually) as periodic-rate. num-periods must be greater than or equal to 0.
payment: A number value representing the payment made or amount received each period. payment is often formatted as currency. At each period, an amount received is a positive amount and an amount invested is a negative amount. For example, it could be a monthly loan payment (negative) or the periodic payment received on an annuity (positive).
future-value: An optional number value that represents the value of the investment or remaining cash value of the annuity (positive amount), or the remaining loan balance (negative amount), after the final payment. future-value is often formatted as currency. At the end of the investment period, an amount received is a positive amount and an amount invested is a negative amount. For example, it could be the balloon payment due on a loan (negative) or the remaining value of an annuity contract (positive). If omitted, future-value is assumed to be 0. If payment is specified and there is no investment value, cash value or loan balance remaining, future-value may be omitted. If payment is omitted, you must include future-value.
when-due: An optional modal value that specifies whether payments are at the beginning or end of each period. Most mortgage and other loans require the first payment at the end of the first period (0), which is the default. Most lease and rent payments, and some other types of payments, are due at the beginning of each period (1).
end (0 or omitted): Payment is treated as being received or made at the end of each period.
beginning (1): Payment is treated as being received or made at the beginning of each period.
Notes
The currency shown in this function result depends on your Language & Region settings (in System Preferences in macOS and in Settings in iOS and iPadOS), or on your Time Zone & Region settings in iCloud Settings.
Example 1 |
|---|
Suppose you would like to help your daughter buy her first house when she is old enough. She has just turned 3 and you expect she will need her own place in 15 years (num-periods is 15*12). You think you will need to have £150,000 (future-value, which is positive because it will be a cash inflow) set aside in a savings account by the time she turns 18. You can add £200 (payment is –200 because this is a cash outflow) to the account at the beginning of each month. Over the next 15 years, the savings account is expected to earn an annual interest rate of 4.5%, and earns interest monthly (periodic-rate is 0.045/12). =PV(0.045/12, 15*12, –200, 150000, 1) returns –£50,227.88, the amount that would need to be deposited today (function returns a negative because the deposit to the savings account today is a cash outflow) so that after 15 years of periodic payments, your account would hold the £150,000 you expect will be required. |
Example 2 |
|---|
Suppose you are considering the purchase of a hypothetical discount security. The security matures in 14 years (num-periods is 14*12) and has a redemption value of £100,000 (future value is positive because this would be a cash inflow at maturity). Another alternative is to leave your money in your money market savings account where it is expected to earn an annual yield of 5.25%, payable monthly (periodic-rate is 0.0525/12) (when-due is 0, and it is not required because there is no payment amount). =PV(0.0525/12, 14*12, 0, 100000, 0) returns –£48,027.48 (the function returns a negative amount because the purchase is a cash outflow), which represents the maximum amount you could pay for the discount security and earn interest at least equivalent to that earned in the money market account. |